Occupation of Iraq (2003–2011)

The Occupation of Iraq (2003–2011) was characterized by a large United States military deployment on Iraqi territory, beginning with the US-led invasion of the country in March 2003 which overthrew the Ba'ath Party government of Saddam Hussein and ending with the departure of US troops from the country in 2011. Troops for the occupation came primarily from the United States, the United Kingdom, and Australia, but 29 other nations also provided troops, and there were varying levels of assistance from Japan and other countries, as well as tens of thousands of private military company personnel.
It was a period of violence and political turmoil, and saw strong foreign influence exerted on Iraqi politics. In April 2003, a military occupation was established and run by the Coalition Provisional Authority (CPA), which later appointed and granted limited powers to the Iraq Interim Governing Council. In June 2004, the Iraqi Interim Government, a caretaker government, was established, ending the international armed conflict between the U.S.-led Coalition and Iraq. Following parliamentary elections in January 2005, this administration was replaced in May by the Iraqi Transitional Government. A year later, the Al Maliki I Government took office.
Efforts toward the reconstruction of Iraq after the damage of the invasion were slowed when coalition and allied Iraqi forces fought a stronger-than-expected militant Iraqi insurgency, leading to difficult living conditions for the population of Iraq throughout the period.
Military occupation
[edit]
A military occupation was established and run by the Coalition Provisional Authority (CPA), which later appointed and granted limited powers to an Iraq Interim Governing Council. Troops for the invasion came primarily from the United States, the United Kingdom, and Australia, but 29 other nations also provided some troops, and there were varying levels of assistance from Japan and other allied countries. Tens of thousands of private security personnel provided protection of infrastructure, facilities and personnel.
Coalition and allied Iraqi forces fought a stronger-than-expected militant Iraqi insurgency, and so the reconstruction of Iraq was slow. In mid-2004, the direct rule of the CPA was ended and a new "sovereign and independent" Interim Government of Iraq assumed the full responsibility and authority of the state. The CPA and the Governing Council were disbanded on 28 June 2004, and a new transitional constitution came into effect.[1]
Sovereignty was transferred to a Governing Council Iraqi interim government led by Iyad Allawi as Iraq's first post-Saddam prime minister; this government was not allowed to make new laws without the approval of the CPA. The Iraqi Interim Government was replaced as a result of the elections which took place in January 2005. A period of negotiations by the elected Iraqi National Assembly followed, which culminated on 6 April 2005 with the selection of, among others, Prime Minister Ibrahim al-Jaafari and President Jalal Talabani. Prime Minister al-Jaafari led the majority party of the United Iraqi Alliance (UIA), a coalition of the al-Dawa and SCIRI (Supreme Council for the Islamic Revolution in Iraq) parties. Both parties are backed by Tehran, and were banned by Saddam Hussein.
Legal status of the coalition presence
[edit]An international armed conflict (IAC) between the United States and Iraq in the Iraq War began when the US-led Coalition invaded Iraq on 19 March 2003. IAC continued after the invasion when the Coalition Provisional Authority (CPA) was established on 21 April to temporarily administer the domestic affairs of Iraq. Therefore, hostilities during the invasion and occupation of Iraq fell under the laws of war applicable to IAC, including the 1949 Geneva Conventions, to which the US and Iraq are parties to, and the 1907 Hague Convention IV - The Laws and Customs of War on Land, which is commonly accepted as customary international humanitarian law binding on non-signatories engaged in an IAC.[2] According to Article 42 under Section III of the Hague Convention IV - The Laws and Customs of War on Land, "[t]erritory is considered occupied when it is actually placed under the authority of the hostile army."[3]
There may be situations where the former occupier will maintain a military presence in the country, with the agreement of the legitimate government under a security arrangement (e.g., US military presence in Japan and Germany). The legality of such agreement and the legitimacy of the national authorities signing it are subject to international recognition, whereby members of the international community re-establish diplomatic and political relations with the national government.
United Nations Security Council Resolution 1546 in 2004 looked forward to the end of the occupation and the assumption of full responsibility and authority by a fully sovereign and independent Interim Government of Iraq.[4] Afterwards, the UN and individual nations established diplomatic relations with the Interim Government, which began planning for elections and the writing of a new constitution. As a result, the Iraq War after 28 June 2004 became a non-international armed conflict (NIAC), since US-led Coalition troops were operating in the country with the consent of the new legitimate government of Iraq. Therefore, hostilities in post-occupation Iraq fell under the laws of war applicable to NIAC, including Common Article 3 of the 1949 Geneva Conventions.
In January 2005, John Negroponte, US ambassador to Iraq, indicated the US government would comply with a United Nations resolution declaring that coalition forces would have to leave if requested by the Iraqi government. "If that's the wish of the government of Iraq, we will comply with those wishes. But no, we haven't been approached on this issue – although obviously we stand prepared to engage the future government on any issue concerning our presence here."[5]
On 10 May 2007, 144 Iraqi Parliamentary lawmakers signed onto a legislative petition calling on the United States to set a timetable for withdrawal.[6] On 3 June 2007, the Iraqi Parliament voted 85 to 59 to require the Iraqi government to consult with Parliament before requesting additional extensions of the UN Security Council Mandate for Coalition operations in Iraq.[7] The UN mandate under United Nations Security Council Resolution 1790 expired on 31 December 2008.
Occupation (21 April 2003 – 28 June 2004)
[edit]An international armed conflict (IAC) between the US and Iraq in the Iraq War began when the US-led Coalition invaded Iraq on 19 March 2003. IAC continued after the invasion when the CPA was established on 21 April to temporarily administer the domestic affairs of Iraq. Therefore, hostilities during the invasion and occupation of Iraq fell under the laws of war applicable to IAC, including the 1949 Geneva Conventions, to which the US and Iraq are parties to, and the 1907 Hague Convention IV - The Laws and Customs of War on Land, which is commonly accepted as customary international humanitarian law binding on non-signatories engaged in an IAC.[2]
2003
[edit]Fall of Saddam Hussein's government
[edit]
Schools, police, courts, government, and military were shut down, which meant that most Iraqis were unemployed.[8] Cities, especially Baghdad, suffered through reductions in electricity, clean water, and telephone service from pre-war levels, with shortages that continued through at least the next year.[9]
On 1 May 2003, President of the United States George W Bush declared the "end of major combat operations" in Iraq, while aboard the USS Abraham Lincoln with a large "Mission Accomplished" banner displayed behind him. The weeks following the removal of Ba'ath Party rule were portrayed by American media as generally a euphoric time among the Iraqi populace. New York Post correspondent Jonathan Foreman wrote from Baghdad in May 2003 that "the intensity of the population's pro-American enthusiasm is astonishing".[10]
There were widespread reports of looting, though much of the looting was directed at former government buildings and other remnants of the former government, and reports of losses of up to 170,000 items of Iraq's archaeological treasures worth billions of US dollars, mostly from the National Museum of Iraq,[11] were later revealed to be vastly exaggerated.[12][13]
Insurgency begins
[edit]
In the summer of 2003, the US military focused on hunting down the remaining leaders of the ousted government, culminating in the killing of Saddam's sons Uday Hussein and Qusay Hussein on 22 July.[14] In all, over 200 top leaders of the former regime were killed or captured, as well as numerous lesser functionaries and military personnel.
After the initial invasion, most of the Iraqi military's former soldiers and officers offered little resistance to Coalition forces in the early days of the occupation. Many soldiers had simply gone home rather than openly fight the invading forces. This seeming acceptance of Coalition authority stemmed from the US military continuing to pay the salaries of Saddam's former soldiers, while promising senior Iraqi officers that they would have a major role to play "in building a new Iraq."
However, on 11 May 2003, the Bush Administration established the "Coalition Provisional Authority" (CPA) to take control of Iraq's domestic affairs away from the US military. Twelve days later, Paul Bremer, head of the CPA, issued an order dissolving the entire Iraqi military, as well as most civilian employees of the old government, and pledged to build a new military and government from scratch. One "untainted by any ties to Saddam's regime," according to the CPA. The Iraqi army's abrupt end, against the protests of many US field commanders, sparked immediate rioting among former Iraqi soldiers. In addition to broader civil unrest as unemployment skyrocketed to 70% and practically every government service, from the police to trash collectors, ended without warning.[15] Soon, large numbers of former Iraqi military personnel allied with the surviving Ba'ath loyalists and formed guerrilla units, igniting an eight-year insurgency against Coalition forces. Besides scattered attacks in Baghdad, these insurgents began to focus on taking and holding ground in and around Mosul, Tikrit, and Fallujah. In the fall of 2003, these largely secular units were joined by religiously motivated "Jihadists" insurgents, both foreign and domestic. With the growing influence of religious fanatics, the insurgency's mostly traditional tactics of sniping, small unit ambushes and planting roadside improvised explosive devices against foreign military personnel began transforming into frequent suicide bombings and death squads targeting civilians that were perceived as "loyal" to coalition forces.[15]
They favored attacking the unarmored Humvee vehicles, and in November they successfully attacked US rotary aircraft with SA-7 missiles bought on the global black market. On 19 August, the UN Headquarters in Baghdad was destroyed in the Canal Hotel Bombing, killing at least 22 people, among them Sérgio Vieira de Mello, Special Representative of the UN Secretary General.
Saddam captured and elections urged
[edit]In December 2003, Saddam himself was captured. The provisional government began training a security force intended to defend critical infrastructure, and the US promised over $20 billion in reconstruction aid in the form of credits against Iraq's future oil revenues. At the same time, elements left out of the Iraqi Patriotic Alliance (IPA) began to agitate for elections. Most prominent among these was Ali al-Sistani, Grand Ayatollah in the Shia sect of Islam.
The United States and the Coalition Provisional Authority, run by Jay Garner and three deputies, including Tim Cross, opposed allowing democratic elections at this time, preferring instead to eventually hand over power to an unelected group of Iraqis.[16] More insurgents stepped up their activities. The two most turbulent centers were the area around Fallujah and the poor Shia sections of cities from Baghdad to Basra in the south.
1 January 2004 – 28 June 2004
[edit]

Spring fighting
[edit]In the spring, the United States and the Coalition Provisional Authority decided to confront the rebels with a pair of assaults: one on Fallujah, the center of the "Mohammed's Army of Al-Ansar", and another on Najaf, home of an important mosque, which had become the focal point for the Mahdi Army and its activities. In Fallujah four private security contractors, working for Blackwater USA, were ambushed and killed, and their corpses desecrated. In retaliation a US offensive was begun, but it was soon halted because of the protests by the Iraqi Governing Council and negative media coverage.
A truce was negotiated that put a former Ba'athist general in complete charge of Fallujah. The 1st Armored Division along with the 2nd ACR were then shifted south, because Spanish, Salvadoran, Ukrainian, and Polish forces were having increasing difficulties retaining control over Al Kut, and Najaf. The 1st Armored Division and 2nd ACR relieved the Spaniards, Salvadoran, Poles, and put down the overt rebellion.
At the same time, British forces in Basra were faced with increasing restiveness, and became more selective in the areas they patrolled. In all, April, May and early June represented the bloodiest months of fighting since the end of hostilities. The Iraqi troops who were left in charge of Fallujah after the truce began to disperse and the city fell back under insurgent control.
In the April battle for Fallujah, US troops killed about 200 resistance fighters, while 40 Americans died and hundreds were wounded in a fierce battle. US forces then turned their attention to the al Mahdi Army in Najaf. A large convoy of US Army supply trucks manned by civilian contractors was ambushed and suffered significant damage and casualties.
Transfer of sovereignty
[edit]On 28 June 2004, under the auspices of United Nations Security Council Resolution 1546, the CPA transferred limited sovereignty to a caretaker government, whose first act was to begin the trial of Saddam Hussein. The transfer marked the end of an IAC between the U.S. and Iraq. The new Iraqi government began the process of moving towards elections, though the insurgency, and the lack of cohesion within the government itself, led to repeated delays.
Militia leader Muqtada al-Sadr used his grass-roots organization and Mahdi Militia of over a thousand armed men to take control of the streets of Baghdad. The CPA soon realized it had lost control and closed down his popular newspaper. This resulted in mass anti-American demonstrations. The CPA then attempted to arrest al-Sadr on murder charges. He defied the American military by taking refuge in the Holy City of Najaf.
Post-occupation (28 June 2004 – 15 December 2011)
[edit]Hostilities between the US and Iraq ended on 28 June 2004 when the CPA handed over Iraqi sovereignty to the Iraqi Interim government as mandated by UN Resolution 1546. Throughout the Iraq War, US-led Coalition troops were operating in the country with the consent of the new legitimate government of Iraq. Therefore, the war in Iraq after 28 June 2004 became a non-international armed conflict (NIAC), which fell under the laws of war applicable to NIAC, including Common Article 3 of the Geneva Conventions.
28 June 2004 – 31 December 2004
[edit]Through July and August, a series of skirmishes in and around Najaf culminated with the Imman Ali Mosque itself under siege, only to have a peace deal brokered by al-Sistani in late August.[17] Al-Sadr then declared a national cease fire, and opened negotiations with the American and government forces. His militia was incorporated into the Iraqi security forces and al-Sadr is now a special envoy. This incident was the turning point in the failed American efforts to install Ahmed Chalabi as leader of the interim government. The CPA then put Iyad Allawi in power; ultimately he was only marginally more popular than Chalabi.
The Allawi government, with significant numbers of holdovers from the Coalition Provisional Authority, began to engage in attempts to secure control of the oil infrastructure, the source of Iraq's foreign currency, and control of the major cities of Iraq. The continuing insurgencies, poor state of the Iraqi Army, disorganized condition of police and security forces, as well as the lack of revenue hampered their efforts to assert control. In addition, both former Ba'athist elements and militant Shia groups engaged in sabotage, terrorism, open rebellion, and establishing their own security zones in all or part of a dozen cities. The Allawi government vowed to crush resistance, using US troops, but at the same time negotiated with Muqtada al-Sadr.
Offensives and counteroffensives
[edit]
Beginning 8 November, American and Iraqi forces invaded the militant stronghold of Fallujah in Operation Phantom Fury, killing and capturing many insurgents. Many rebels were thought to have fled the city before the invasion. US-backed figures put insurgency losses at over 2,000. It was the bloodiest single battle for the US in the war, with 92 Americans dead and several hundred wounded. A video showing the killing of at least one unarmed and wounded man by an American serviceman surfaced, throwing renewed doubt and outrage at the efficiency of the US occupation.[18] The Marine was later cleared of any wrongdoing because the Marines had been warned that the enemy would sometimes feign death and booby-trap bodies as a tactic to lure Marines to their deaths. November was the deadliest month of the occupation for coalition troops, surpassing April.
Another offensive was launched by insurgents during the month of November in Mosul. US forces backed by peshmerga fighters launched a counteroffensive which resulted in the Battle of Mosul (2004). The fighting in Mosul occurred concurrently with the fighting in Fallujah and attributed to the high number of American casualties taken that month.
In December, 14 American soldiers were killed and over a hundred injured when an explosion struck an open-tent mess hall in Mosul, where President Bush had spent Thanksgiving with troops the year before. The explosion is believed to have come from a suicide bomber.
After a review of the military strategy in the end of 2004, then commanding general of the MNF-I, General George Casey directed the Coalition forces to shift their focus from fighting insurgents to training Iraqis.[19] At the time, the Iraqi insurgency was mainly directed against the occupation and it was believed that if the Coalition would reduce its presence then the insurgency would diminish. Military planners hoped that national elections would change the perception of being under occupation, stabilize the situation and allow the Coalition to reduce its presence.
2005
[edit]Iraqi elections and aftermath
[edit]
On 30 January, an election for a government to draft a permanent constitution took place. Although some violence and lack of widespread Sunni Arab participation marred the event, most of the eligible Kurd and Shia populace participated. On 4 February, Paul Wolfowitz announced that 15,000 US troops whose tours of duty had been extended in order to provide election security would be pulled out of Iraq by the next month.[20] February, March and April proved to be relatively peaceful months compared to the carnage of November and January, with insurgent attacks averaging 30 a day from the average 70.
Hopes for a quick end to an insurgency and a withdrawal of US troops were dashed at the advent of May, Iraq's bloodiest month since the invasion of US forces in March and April 2003. Suicide bombers, believed to be mainly disheartened Iraqi Sunni Arabs, Syrians and Saudis, tore through Iraq. Their targets were often Shia gatherings or civilian concentrations mainly of Shias. As a result, over 700 Iraqi civilians died in that month, as well as 79 US soldiers.

During early and mid-May, the US also launched Operation Matador, an assault by around 1,000 Marines in the ungoverned region of western Iraq. Its goal was the closing of suspected insurgent supply routes of volunteers and material from Syria, and with the fight they received their assumption proved correct. Fighters armed with flak jackets (unseen in the insurgency by this time) and sporting sophisticated tactics met the Marines, eventually inflicting 30 US casualties by the operation's end, and suffering 125 casualties themselves.
The Marines succeeded, recapturing the whole region and even fighting insurgents all the way to the Syrian border, where they were forced to stop (Syrian residents living near the border heard the American bombs very clearly during the operation). The vast majority of these armed and trained insurgents quickly dispersed before the US could bring the full force of its firepower on them, as it did in Fallujah.
Announcements and renewed fighting
[edit]On 14 August 2005 the Washington Post quoted one anonymous US senior official expressing that "the United States no longer expects to see a model new democracy, a self-supporting oil industry or a society in which the majority of people are free from serious security or economic challenges... 'What we expected to achieve was never realistic given the timetable or what unfolded on the ground'".[21]
On 22 September 2005, Prince Saud al-Faisal, the Saudi foreign minister, said he had warned the Bush administration that Iraq was hurtling toward disintegration, and that the election planned for December was unlikely to make any difference.[22] US officials immediately made statements rejecting this view.[23]
Constitutional ratification and elections
[edit]The National Assembly elected in January had drafted a new constitution to be ratified in a national referendum on 15 October 2005. For ratification, the constitution required a majority of national vote, and could be blocked by a two-thirds "no" vote in each of at least three of the 18 governorates. In the actual vote, 79% of the voters voted in favor, and there was a two-thirds "no" vote in only two governorates, both predominantly Sunni. The new Constitution of Iraq was ratified and took effect. Sunni turnout was substantially heavier than for the January elections, but insufficient to block ratification.
Elections for a new Iraqi National Assembly were held under the new constitution on 15 December 2005. This election used a proportional system, with approximately 25% of the seats required to be filled by women. After the election, a coalition government was formed under the leadership of Prime Minister Nouri al-Maliki, with Jalal Talabani as president.
2006
[edit]The beginning of that year was marked by government creation talks and continuous anti-coalition and attacks on mainly Shia civilians.
Al-Askari shrine bombing and Sunni-Shia fighting
[edit]
'Alī an-Naqī and Hasan al-'Askarī
On 22 February 2006. bombs exploded at the Al Askari Mosque causing substantial damage.
On 2 March the director of the Baghdad morgue fled Iraq explaining, "7,000 people have been killed by death squads in recent months."[24] The Boston Globe reported that around eight times the number of Iraqis killed by terrorist bombings during March 2006 were killed by sectarian death squads during the same period. A total of 1,313 were killed by sectarian militias while 173 were killed by suicide bombings.[25] The LA Times later reported that about 3,800 Iraqis were killed by sectarian violence in Baghdad alone during the first three months of 2006. During April 2006, morgue numbers show that 1,091 Baghdad residents were killed by sectarian executions.[26]
Insurgencies, frequent terrorist attacks and sectarian violence in Iraq lead to harsh criticism of US policy and fears of a failing state and civil war. The concerns were expressed by several US think tanks[27][28][29][30] as well as the US ambassador to Iraq, Zalmay Khalilzad.[31]
In early 2006, a handful of high-ranking retired generals began to demand Secretary of Defense Rumsfeld's resignation due in part to the aforementioned chaos that apparently resulted from his management of the war.
British hand Muthanna province to Iraqis
[edit]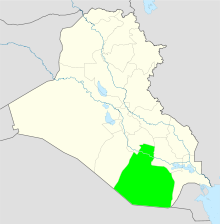
On 12 July 2006, Iraq took full control of the Muthanna province, marking the first time since the invasion that a province had been handed from foreign troops to the Iraqi government. In a joint statement, the US ambassador Zalmay Khalilzad and the US commander in Iraq, General George Casey, hailed it as a milestone in Iraq's capability to govern and protect itself as a "sovereign nation" and said handovers in other provinces will take place as conditions are achieved. "With this first transition of security responsibility, Muthanna demonstrates the progress Iraq is making toward self- governance", the statement said, adding that "Multi-National Forces will stand ready to provide assistance if needed." At the ceremony marking the event, Iraqi Prime Minister Nouri al-Maliki stated, "It is a great national day that will be registered in the history of Iraq. This step forward will bring happiness to all Iraqis."[32][33]
Forward Operating Base Courage handed over to Nineveh province government
[edit]
A former presidential compound of Saddam Hussein, dubbed Forward Operating Base Courage by Coalition forces, was handed over by Charlie Company 4-11FA to the Nineveh province government on 20 July 2006. The main palace had been home to the 101st Airborne Division Main Command Post, Task Force Olympia CP, 4-11FA of the 172nd SBCT, and the Task Force Freedom CP. The palace served as the last command post for the Multinational Force-Iraq–Northwest. US soldiers had spent the summer restoring the palace for the eventual handover.
Major General Thomas R. Turner II, commanding general, Task Force Band of Brothers stated at a ceremony marking the occasion "The turnover of Forward Operating Base Courage is one of the larger efforts towards empowering the Iraqi people and represents an important step in achieving Iraqi self-reliance ... The gains made during the past three years demonstrate that the provincial government, the Iraqi Army and the Iraqi Police are increasing their capabilities to take the lead for their nation's security." Duraid Kashmoula, the governor of the Nineveh Governorate, stated after being handed the key to the palace "Now this palace will be used to benefit the Iraqi government and its people."[34][35]
British troops leave Camp Abu Naji
[edit]
On 24 August 2006, Maj Charlie Burbridge, a British military spokesman, said the last of 1,200 British troops left Camp Abu Naji, just outside Amarah in Iraq's southern Maysan province. Burbridge told Reuters that British troops leaving the base were preparing to head deep into the marshlands along the Iranian border, stating "We are repositioning our forces to focus on border areas and deal with reports of smuggling of weapons and improvised explosive devices from across the border."
The base had been a target for frequent mortar and rocket barrages since being set up in 2003, but Burbridge dismissed suggestions the British had been forced out of Amara while acknowledging the attacks had been one reason for the decision to withdraw, the second being that a static base did not fit with the new operation. "Abu Naji was a bulls-eye in the middle of a dartboard. The attacks were a nuisance and were a contributing factor in our planning", to quit the base, he said, adding "By no longer presenting a static target, we reduce the ability of the militias to strike us ... We understand the militias in Maysan province are using this as an example that we have been pushed out of Abu Naji, but that is not true. It was very rare for us to take casualties." Burbridge stated that Iraqi security forces would now be responsible for day-to-day security in Maysan but stressed that the British had not yet handed over complete control to them.
Muqtada al-Sadr called the departure the first expulsion of US-led coalition forces from an Iraqi urban center. A message from al-Sadr's office that played on car-mounted speakers throughout Amarah exclaimed "This is the first Iraqi city that has kicked out the occupier ... We have to celebrate this occasion!" A crowd of as many as 5,000 people, including hundreds armed with AK-47 assault rifles, ransacked Camp Abu Naji immediately after the last British soldier had departed despite the presence of a 450-member Iraqi army brigade meant to guard the base. The looting, which lasted from about 10 am to early evening, turned violent at about noon when individuals in the mob shot at the base.
The Iraqi troops asked the province's governor for permission to return fire, a decision the British military highlighted as evidence of the security force's training. "It demonstrated that they understand the importance of civilian primacy, that the government – and not the military – is in charge", Burbridge said in a phone interview with The Washington Post. Injuries were reported on both sides, but no one was killed. Burbridge attributed the looting to economic factors rather than malice, stating "The people of Amarah – many of whom are extremely poor – saw what they believed to be a bit of an Aladdin's cave inside." Some residents of Amarah, however, told the Post that antipathy toward the occupation was strong. "The looters stole everything – even the bricks ... They almost leveled the whole base to the ground", said 20-year-old student at Maysan University Ahmed Mohammed Abdul Latief.[36][37][38]
Situation in and around Baghdad
[edit]


On 28 August 2006, one US general said violence in Baghdad had fallen by nearly a half since July, although he acknowledged a spike in bombings in the past 48 hours. "Insurgents and terrorists are hitting back in an attempt to offset the success of the Iraqi government and its security forces", Maj Gen William Caldwell told reporters. After meeting Iraqi Defence Minister Abdul-Qader Mohammed Jassim al-Mifarji, British Secretary of State for Defence Des Browne said Iraq was moving forward, and that "each time I come, I see more progress".[39]
The American military command acknowledged in the week of 16 October 2006 that it was considering an overhaul of its latest security plan for Baghdad, where three months of intensive American-led sweeps had failed to curb violence by Sunni Arab-led insurgents and Shiite and Sunni militias.[40]
Numerous car and roadside bombs rocked the capital 9 November 2006 morning: In the Karrada district, a car bomb killed six and wounded 28 others. Another car bomb killed seven and wounded another 27 in the northern Qahira neighborhood. In South Baghdad, a mortar then a suicide car bomber killed seven and wounded 27 others near the Mishin bazaar. Near the college of Fine Arts in north-central Baghdad, a car bomb targeting an Iraqi patrol killed three and wounded six others. Two policemen were injured when they tried to dismantle a car bomb in the Zayouna district. A car bomb on Palestine Street in northeastern Baghdad meant for an Iraqi patrol killed one soldier but also wounded four civilians. Yet another car bomb in southern Baghdad wounded three people. And another car bomb near a passport services building in a northern neighborhood killed 2 people and wounded 7 others.
A roadside bomb in central Baghdad killed two and wounded 26 others. A police patrol was blasted by a roadside bomb near a petrol station; four were killed in the explosion. Another four people were wounded in the New Baghdad neighborhood by yet another roadside bomb. A bomb hidden in a sack exploded in Tayern square killing three and wounding 19. Another bomb in the Doura neighborhood killed one and wounded three. Mortars fell in Kadmiyah killing one woman and injuring eight people, and in Bayaladat where four were wounded.
Also in the capital, a group of laborers were kidnapped in the morning of 9 November 2006; five bodies were recovered later in the Doura neighborhood, but at least one other body was found in Baghdad that day. Gunmen also killed a police colonel and his driver in the east of the city. And just outside town, police arrested two people in a raid and discovered one corpse.[41]
On 10 November, Iraqi police recovered 18 bullet-riddled bodies in various neighborhoods around the capital which the police were unable to identify. The following day, two bombs planted in an outdoor market in central Baghdad exploded around noon, killing six and wounded 32 people. A car bomb and a roadside bomb were detonated five minutes apart in the market, which is in an area close to Baghdad's main commercial center. The US military said it has put up a $50,000 reward for anyone who helps find an American soldier kidnapped in Baghdad. The 42-year-old Army Reserve specialist, Ahmed al-Taie, was abducted on 23 October when he left the Green Zone, the heavily fortified section where the United States maintains its headquarters, to visit his Iraqi wife and family.
A suicide bomber killed 40 Iraqis and wounded 70 on 12 November 2006 morning outside the national police headquarters' recruitment center in western Baghdad, an emergency police official said. They were among dozens of men waiting to join the police force in the Qadessiya district when a suicide bomber detonated an explosives belt. In central Baghdad, a car bomb and roadside bomb killed four Iraqi civilians and wounded 10 near the Interior Ministry complex. And in the Karrada district of central Baghdad, one Iraqi was killed and five were wounded when a car bomb exploded near an outdoor market 12 November 2006 morning. Gunmen shot dead an Iraqi officer with the new Iraqi intelligence system as he was walking towards his parked car in the southwestern Baghdad neighborhood of Bayaa. Two civilians were killed and four more were wounded when a roadside bomb hit a car in the eastern Baghdad neighborhood of Zayuna.[42]
Violent incidents in other cities
[edit]9 November 2006.[41]
- Suwayrah: Four bodies were recovered from the Tigris River. Three of them were in police uniforms.
- Amarah: A roadside bomb killed one and wounded three others in Amarah. Gunmen also shot dead a suspected former member of the Fedayeen paramilitary.
- Muqdadiyah: Gunmen stormed a primary school and killed three: a guard, a policeman and a student.
- Tal Afar: A roadside bomb in Tal Afar killed four, including a policeman, and wounded eight other people. Two policemen were killed and four civilians were injured when a rocket landed in a residential neighborhood.
- Mosul: Six people were shot dead, including one policeman.
- Latifiya: Four bodies, bound and gagged, were discovered.
- Baqubah: Eight people were killed in different incidents.
11 November 2006.[43]
- Latifiya: Gunmen killed a truck driver and kidnapped 11 Iraqis after stopping four vehicles at a fake checkpoint south of the capital. At the fake checkpoint in Latifiya, about 25 miles (40 km) south of Baghdad, gunmen took the four vehicles—three minibuses and a truck—along with the kidnapped Iraqis. The Iraqis—11 men and three women—were driving from Diwaniya to Baghdad for shopping when they were stopped. The gunmen left the three women and kidnapped the 11 men, the official said.
- Baqubah: North of the capital near Baquba, a suicide car bomb explosion killed two people at the main gate of a police station in Zaghanya town.
Al-Qaeda
[edit]

Although Saddam Hussein was accused of having links to Al-Qaeda members, only a few Al-Qaeda members were found hiding in Iraq before the invasion, and all were of lower standings.
On 3 September 2006, Iraq says it has arrested the country's second most senior figure in Al-Qaeda, "severely wounding" an organization the US military says is spreading sectarian violence that could bring civil war. The National Security Adviser Mowaffak al-Rubaie summoned reporters to a hastily arranged news conference to announce that al Qaeda leader Hamid Juma Faris al-Suaidi had been seized some days ago. Hitherto little heard of, and also known as Abu Humam or Abu Rana, Suaidi was captured hiding in a building with a group of followers. "Al-Qaeda in Iraq is severely wounded", Rubaie said. He said Suaidi had been involved in ordering the bombing of the Shi'ite shrine in Samarra in February 2006 that unleashed the wave of tit-for-tat killings now threatening civil war. Iraqi officials blame Al-Qaeda for the attack. The group denies it. Rubaie did not give Suaidi's nationality. He said he had been tracked to the same area north of Baghdad where US forces killed Al-Qaeda's leader Abu Musab al-Zarqawi in June 2006. "He was hiding in a building used by families. He wanted to use children and women as human shields", Rubaie said. Little is publicly known about Suaidi. Rubaie called him the deputy of Abu Ayyub al-Masri, a shadowy figure, probably Egyptian, who took over the Sunni Islamist group from Zarqawi.[44]
The US military says Al-Qaeda is a "prime instigator" of the violence between Iraq's Sunni minority and Shi'ite majority but that US and Iraqi operations have "severely disrupted" it.[44]
A handover ceremony on 2 September 2006 was postponed at the last minute, first to 3 September 2006, then indefinitely, after a dispute emerged between the government and Washington over the wording of a document outlining their armies' new working relationship. "There are some disputes", an Iraqi government source said. "We want thorough control and the freedom to make decisions independently." US spokesman Lieutenant Colonel Barry Johnson played down any arguments and expected a signing soon: "It is embarrassing but it was decided it was better not to sign the document." Practically, US troops remain the dominant force. Their tanks entered the southern, Shi'ite city of Diwaniya on 3 September 2006. The show of force came a week after Shi'ite militiamen killed 20 Iraqi troops in a battle that highlighted violent power struggles between rival Shi'ite factions in the oil-rich south.[44]
Abu Ghraib
[edit]On 2 September 2006, the Abu Ghraib prison was formally handed over to Iraq's government. The formal transfer was conducted between Lieutenant General Jack Gardner, Commander of Task Force 134, and representatives of the Iraqi Ministry of Justice and the Iraqi Army.[45]
Iraqi government takes control of the 8th Iraqi Army Division
[edit]
On 7 September 2006, Prime Minister Nouri al-Maliki signed a document taking control of Iraq's small naval and air forces and the 8th Iraqi Army Division, based in the south. At a ceremony marking the occasion, Gen George Casey, the top US commander in Iraq stated "From today forward, the Iraqi military responsibilities will be increasingly conceived and led by Iraqis." Previously, the US-led Multi-National Force – Iraq, commanded by Casey, gave orders to the Iraqi armed forces through a joint American-Iraqi headquarters and chain of command. After the handover, the chain of command flows directly from the prime minister in his role as Iraqi commander in chief, through his Defense Ministry to the Iraqi Joint Forces Command. From there, the orders go to Iraqi units on the ground. The other nine Iraqi division remained under US command, with authority gradually being transferred. US military officials said there was no specific timetable for the transition.[46]
Anbar province reported as politically "lost" to US and Iraqi government
[edit]

On 11 September 2006, it transpired that Colonel Peter Devlin, chief of intelligence for the Marine Corps in Iraq, had filed a secret report, described by those who have seen it as saying that the US and the Iraqi government have been defeated politically in Anbar province. According to The Washington Post, an unnamed Defense Department source described Devlin as saying "there are no functioning Iraqi government institutions in Anbar, leaving a vacuum that has been filled by the insurgent group al-Qaeda in Iraq, which has become the province's most significant political force." The Post said that Devlin is a very experienced intelligence officer whose report was being taken seriously.[47]
The next day, Major General Richard Zilmer, commander of the Marines in Iraq, stated: "We are winning this war... I have never heard any discussion about the war being lost before this weekend."[48]
In the fall of 2006 several Iraqi tribes near Ramadi led by Sheikh Abdul Sattar Abu Risha revolted against various insurgent groups with Al Qaeda in Iraq. They formed the Anbar Awakening and helped turn the tide in favor of the US military.
Two more provinces were transferred to Provincial Iraqi Control in late 2006.
On 21 September 2006, Italian troops handed security control of the Dhi Qar province to Iraqi forces, making Dhi Qar the second of the country's 18 provinces to come under complete local control. A transfer ceremony was carried out in Nasiriyah.[49]
On 20 December 2006, US forces handed over control of the southern province of Najaf to Iraqi security forces.[50]
2007
[edit]
In January 2007 US President George W. Bush announced a "Surge" in the number of US troops deployed to the country.[51] Also in early 2007, US and Iraqi tribal forces secured Ramadi, as well as other cities such as Hit, Haditha, Rutbah, and Al Qaim.
In May 2007, Iraq's Parliament called on the United States to set a timetable for withdrawal[52] and US coalition partners such as the UK and Denmark began withdrawing their forces from the country.[53][54] During the summer the US turned its attention to eastern Anbar and secured the cities of Fallujah and Al-Karmah.
Celebrating victory, President George W. Bush flew to Anbar in August 2007 to congratulate Sheik Sattar and other leading tribal figures.
2008
[edit]Iraqi forces begin process of arming with advanced US weapon systems
[edit]
Iraq became one of the top current purchasers of US military equipment with their army trading its AK-47 assault rifles for the more accurate US M16 and M4 rifles, among other equipment.[55]
Iraq sought 36 F-16's, the most sophisticated weapons system Iraq has attempted to purchase. The Pentagon notified Congress that it had approved the sale of 24 American attack helicopters to Iraq, valued at as much as $2.4 billion. Including the helicopters, Iraq announced plans to purchase at least $10 billion in US tanks and armored vehicles, transport planes and other battlefield equipment and services. Over the summer, the Defense Department announced that the Iraqi government wanted to order more than 400 armored vehicles and other equipment worth up to $3 billion, and six C-130J transport planes, worth up to $1.5 billion.[56]
In 2008 Iraq accounted for more than $12.5 billion of the $34 billion US weapon sales to foreign countries (not including the potential F-16 fighter planes).[57]
2009
[edit]Vice President of the United States Joe Biden made his second visit to Baghdad in as many months in September 2009, and met with Prime Minister Nouri al-Maliki even as insurgents fired mortars and rockets at the Green Zone to protest his presence. Although said to be in "listening mode", Biden addressed issues of security, political reconciliation, and foreign investment in Iraq's oil-rich but weakened economy with various leaders in the capital and Iraq's Kurdish region.[58] "We will also move ahead on other aspects of our security agreement by removing all US combat brigades from Iraq by the end of August 2010 and all remaining US troops by the end of 2011," Biden said.[59]
2010
[edit]Final departure of US combat troops
[edit]
On 18 August 2010 the final US combat troops were reported to have crossed the border into Kuwait, when a last convoy of the Army's 4th Stryker Brigade Combat Team departed Iraq. A spokesman for the US State Department, P. J. Crowley, was quoted by news media as saying the departure was "a historic moment," but noted that the US presence in Iraq would continue. The pullout of combat forces was nearly two weeks ahead of the announced deadline of 31 August.
In a released statement, US President Obama said of the withdrawn soldiers, "I hope you'll join me in thanking them, and all of our troops and military families, for their service." He noted that the event was a "milestone in the Iraq war."[60]
The closure of Operation Iraqi Freedom was announced on 31 August. "It is time to turn the page," Obama said in a national address. The operations in Iraq were renamed "New Dawn".
Participating nations
[edit]As of May 2011, the United States was the only country with military forces stationed in Iraq. Other nations also present but under the United Nations banner.[61]
As of September 2006, there were an estimated 145,000 US troops in Iraq.[62] There are also approximately 20,000 private security contractors of different nationalities under various employers.
Casualties
[edit]Iraqi councils and authorities
[edit]On 11 October 2002, President Bush's senior adviser on the Middle East, Zalmay Khalilzad, released US government plans to establish an American-led military administration in Iraq, as in post-war Germany and Japan, which could last for several years after the fall of Saddam.[63] In the run-up to the invasion, the US promised a speedy transition to a democratic government, as well as the creation of an Iraqi constitution, and the active role of Iraqis in the establishment of an interim authority and new government. US officials continue to emphasize that the invasion was not about long-term occupation, but about liberation.

In November 2003, Paul Bremer announced the plan to hand over limited sovereignty to the Iraqi governing council by 30 June 2004. A draft constitution was written and approved by the Iraqi Governing Council in March 2004. The United States has stated its plans to enter into what it calls a security agreement with the new Iraqi government and maintain military authority until a new Iraqi army is established. The Bush administration remained committed to this date despite the unstable security situation. The interim Iraqi government was named in May 2004, at which point the Iraqi Governing Council was dissolved, though there was heavy overlap between the two governing bodies.
The US-led Coalition Provisional Authority, for administrative purposes, divided Iraq into four security zones (see map): a North zone in the Mosul – Kirkuk region, a Central zone in the Baghdad – Tikrit region, a Southern Central zone in the Karbala region and a South zone in the Basra region. The northern and central zones were garrisoned by US troops, while the Southern Central zone was garrisoned by a Multi-National Division under Polish command and the South zone was garrisoned by a Multi-National Division under British command.[64]
In the early months of the occupation, looting and vandalism slowed the restoration of basic services such as water, electricity, and sanitation. By Spring 2004, these services were mostly restored to pre-war levels. Uneven power distribution remained a problem through 2004, with the Baghdad area continuing to have periodic blackouts.[65] On 28 July 2005, Iraq's Electricity Minister announced that Iraq's electricity supply had risen to above pre-war levels.[66]
Numerous allegations were made of human rights violations by the occupying forces in post-invasion Iraq. One of the most significant of these was the Abu Ghraib torture and prisoner abuse scandal, where 11 American soldiers from the 372nd Military Police Company were convicted in 2005 for a series of war crimes over the mistreatment of Iraqi prisoners. The Bush administration denied that the abuses were indicative of US military policy in Iraq.[67][68]
Former Ba'ath Party members and military officers who have no criminal past or human rights abuses have been allowed to return to government positions.[69]
Reconstruction
[edit]For the reconstruction, contracts were awarded to private companies. Initially companies from countries that had opposed the war were excluded from these contracts, but this decision was reversed due to protests.[70] Political activists and commentators allege that The Pentagon favoured companies like Halliburton, former employer of Vice President Dick Cheney, because they had connections to high-ranking members of the Bush administration.[71][72] This suspicion had already been a concern during the global protests against the war on Iraq. An audit found that Halliburton subsidiary Kellogg, Brown and Root (KBR) may have overcharged the US government $61 million, on contracts worth billions, for bringing oil products for the US army into Iraq via a Kuwaiti subcontractor, Altanmia Commercial Marketing Co.[73]
Some also argue that foreign contractors are doing work which could be done by unemployed Iraqis, which might be a factor fueling resentment of the occupation.[74][75][76] Further resentment could be inflamed with the news that almost US$9 billion dollars of Iraqi oil revenue is missing from a fund set up to reconstruct Iraq.[77]
On 14 August 2005, a Washington Post story[78] on the administration's effort to lower expectations, quoted Wayne White, former head of the State Department's Iraq intelligence team, as saying "The most thoroughly dashed expectation was the ability to build a robust self-sustaining economy. We're nowhere near that. State industries, electricity are all below what they were before we got there."
A report of the United States Special Inspector General for Iraq Reconstruction found widespread "fraud, incompetence and confusion" in the American occupation's handling of billions of dollars of Iraqi government money and American funds given for reconstruction. Inspector-general Stuart Bowen, Jr. noted that only 49 of 136 planned water- and sanitation-related projects will be completed.[79]
In April 2007, the New York Times reported that US federal oversight inspectors found that "in a sampling of eight projects that the United States had declared successes, seven were no longer operating as designed because of plumbing and electrical failures, lack of proper maintenance, apparent looting, and expensive equipment that lay idle. The United States has sometimes admitted ... that some of its reconstruction projects have been abandoned, delayed, or poorly constructed. But this is the first time inspectors have found that projects officially declared as successes—in some cases, as little as six months before the latest inspections—were no longer working properly."[80]
In 2012, Iraq bought electricity from the United Arab Emirates, as Iraqis continued to endure electricity cuts of up to twenty hours a day during peak periods of demand,[81] while the country's university system was one of the worst in the Middle East.[82] June saw Prince Abdul Ilah Al Qasim comment that Iraqi oil production was at its highest in twenty years. Abdul Ilah by telephone from Baghdad said that the "oil production has exceeded 3.07 million barrels this month, compared with 2.92 million barrels for the month of May which was announced in the monthly report of OPEC".[83]
Civilian government
[edit]The establishment of a new civilian government of Iraq was complicated by religious and political divisions between the majority Shi'ite population and the formerly ruling Sunni Arabs. Moreover, many of the people in Saddam's ruling Ba'ath Party were perceived as tainted by the association by some parties. In northern Iraq, Kurds had already had effectively autonomous rule for 12 years under the protection of the no-fly zone.
On 16 May 2003, US officials abandoned the plan to cede authority to a democratically chosen interim civilian Iraqi government (similar to what had happened in Afghanistan following the 2001 US invasion) and presented a resolution to the UN to give the United States and the United Kingdom broad power and to lift economic sanctions on Iraq, allowing the occupying countries authority to use oil resources to pay for rebuilding the country. Passage of the resolution allowed them to appoint an interim government by themselves.
On 13 July 2003, an Iraqi Governing Council was appointed by Coalition Provisional Authority Administrator Paul Bremer.
United Nations resolutions
[edit]
On 22 May 2003, the UN Security Council voted 14–0 to give the United States and Britain the power to govern Iraq and use its oil resources to rebuild the country. Resolution 1483 removed nearly 13 years of economic sanctions originally imposed after Iraq's 1990 invasion of Kuwait. The resolution allows UN Secretary-General Kofi Annan to appoint a special representative to work with US and British administrators on reconstruction, humanitarian aid, and the creation of a new government.
The resolution also created the Development Fund for Iraq, which collected funds from oil sales. The fund was initially run by the United States and Britain to rebuild the country, and is overseen by a new advisory body composed of the United Nations and international financial institutions. In June 2004, the New York Times reported that American authorities spent $2.5 billion from Iraqi oil revenue despite agreements that the oil revenues should be set aside for use after the restoration of Iraq's sovereignty.[84]
On 14 August 2003, the Security Council voted 14–0 to "welcome" the creation of the Iraqi Governing Council. Resolution 1500 stopped short of formally recognizing the governing council as Iraq's legitimate governing body but called it an "important step" towards creating a sovereign government.
Elections
[edit]
For several months the United States maintained that it intended to convene a constitutional convention, composed of influential Iraqis. However, European demands for an early election and Ayatollah Ali al-Sistani's insistence eventually forced the United States to let the appointed Governing Council serve this function.
In the early months of the occupation, new officials were appointed to several local and regional positions (e.g., mayors, governors, local councils). The officials were chosen from a select group of individuals (including ex-Ba'ath party officials) in an attempt to speed the return to normality and to avoid the election of people opposed to the Coalition presence. Certain religious clerics and other officials were considered to be overly radical or dangerous. On occasion the appointed officials were found to behave less than admirably. On 30 June 2003, the appointed mayor of Najaf was arrested on charges of corruption.
By February 2004, democratic elections, under the supervision of the CPA, had already been held at the municipal and city level in some of the southern and northern provinces.[85]
On 15 November, the Iraqi Governing Council announced that a transitional government would take over in June from the US-led powers, and that an elected government would follow by the end of 2005 once a constitution had been drafted and ratified. The transitional government would be selected in June 2004 by a transitional council formed in May 2004.
The Governing Council revealed the timetable after the United States government, in reaction to terrorist and militant activity against occupying troops and aid organisations, abandoned its earlier plan that a sovereign government would take charge only after creating a constitution and elections held. Jalal Talabani, who was chairman of the council, said the transition would involve "the creation of a permanent constitution by an elected council, directly elected by the people, and also the election of a new government according to the articles of this new constitution before the end of 2005."
In March 2004, an interim constitution was created, called the Law of Administration for the State of Iraq for the Transitional Period. The document called for the creation of an elected National Assembly to take place no later than January 2005. The question of the election calendar became a matter of importance for Iraq and the US: while a quick election would legitimise the Iraqi government and shed a favourable light on the US-led occupation of the country, the prospect of violence delayed it. It was finally set for 30 January 2005. Though then-President Ghazi Al-Yaouar asked the United Nations to reconsider the electoral schedule several weeks before the election, the legislative election was held on time, creating the Iraqi National Assembly.
The elected assembly drafted a new constitution for Iraq, submitting it to the Iraqi people for review on 28 August. On 15 October, Iraqis voted to approve the new constitution. On 15 December, the first legislative election under the new constitution was held.
Sovereignty for Iraq
[edit]
In a 1 June 2004, press conference, President Bush said that he was working with various world leaders to create a UN Security Council resolution endorsing the transition from the US-dominated occupation to complete autonomy for Iraq. Under this resolution, Coalition forces would remain in Iraq until the new government could establish security and stabilization: "There is a deep desire by the Iraqis – don't get me wrong – to run their own affairs and to be in a position where they can handle their own security measures." On 8 June, Security Council resolution 1546 was adopted unanimously, calling for "the end of the occupation and the assumption of full responsibility and authority by a fully sovereign and independent Interim Government of Iraq by 30 June 2004."
On 28 June 2004, the occupation was nominally ended by the CPA, which transferred limited power to a new Iraqi government led by Prime Minister Iyad Allawi. The multinational military alliance continued to assist the Allawi government in governing the Iraqis. The purpose of the Occupation of Iraq was, according to US President George W. Bush, purely to bring about a transition from post-war anarchy to full Iraqi sovereignty.
A further milestone in sovereignty was achieved with the creation of a democratically elected administration on 6 April 2005 including Prime Minister Ibrahim al-Jaafari and President Jalal Talabani following the Iraqi elections of January 2005.
Under United Nations Security Council Resolution 1790, the mandate of the multinational force in Iraq was extended until 31 December 2008, after which there is no justification for foreign militaries to remain in the country. On 6 June 2008, the Independent reported that the United States was applying pressure to the government of Iraq to sign a "strategic alliance" (not a "treaty", which would require approval of the US senate), giving US forces broad freedom in continuing to operate in Iraq.[86]
Provincial Iraqi control
[edit]The objective of the Iraqi Government and Multi-National Forces in Iraq is to achieve the transition of responsibility for each of the 18 provinces in Iraq from the Coalition to the Iraqi civil authorities, both national and local. Most attention on the issue is understandably focused on progress towards security within the provinces, both in terms of the threat from insurgents and the capability of the Iraqi Security Forces, but other factors, such as the competence and capacity of local governance is also important.[citation needed]
Provinces are subject to regular assessment by the Iraqi government and the Coalition; when a province appears to be ready, a recommendation is made to the Iraqi Ministerial Committee for National Security, with the Prime Minister making the final decision.
Provinces under Iraqi Control
[edit]As of October 2008, thirteen provinces had successfully completed transition to provincial Iraqi control: Muthanna, Dhi Qar, Najaf, Maysan, Dahuk, Erbil, Sulaymaniyah, Karbala, Basra, Al-Qādisiyyah, Al Anbar, Babil and Wasit.
Muthanna was the first, on 13 July 2006, when Australian, Japanese and British forces from Multi-National Division-South East transferred responsibility to the Governor and local authorities. With a small and homogeneous Shia population, there had been very little militia violence and few attacks on Coalition forces in the preceding months, encouraging good progress in developing the capacity of the Iraqi armed forces and Ministry of Interior forces there. Equally, the Governor of Muthanna enjoyed a good local mandate, having been re-elected in local elections in January 2005.[87]
Dhi Qar, also within the area of responsibility of the British-led MND-SE and the responsibility of the Italian and Romanian brigade, was handed over on 21 September 2006. .[88] Australian troops in MND-SE remained available to provide security support to the Iraqis in both Muthanna and Dhi Qar, should they request it.
Najaf, which had been garrisoned by first Polish, then US forces, was handed over on 20 December 2006.[89]
In April 2007, Maysan Governorate became the fourth to transition to provincial Iraqi control. [90]
On 30 May 2007, the three provinces making up the Kurdistan Regional Government transitioned to provincial Iraqi control, bringing the total count to 7. [91]
In October 2007, Karbala became the eighth province to transfer to provincial Iraqi control. The transfer of Basra in December 2007 marked the half-way point in transferring all provincial security over to Iraqi security forces.[92]
In July 2008 the tenth province, Al-Qādisiyyah, also transferred to Iraqi control.[92]

On 1 September 2008, in the wake of the decreasing levels of violence, the US Army transferred control of the expansive Al-Anbar province over to Provincial Iraqi Control. A limited US presence will be maintained to ensure security. Al-Anbar is the 11th province to be transferred to Iraqi security.
In October 2008, Babil province became the twelfth province to return to Iraqi control,[93] whilst Wasit was transferred later in the month, making it the thirteenth province to be transferred.[94]
Transition after Security Agreement signed
[edit]As of 31 December 2008, 13 of Iraq's 18 provinces had successfully transitioned to Provincial Iraqi Control (PIC).[95] On 1 January 2009, the SA (see also US–Iraq Status of Forces Agreement) between the US and Iraq went into effect, transferring security responsibility to the GoI, even though not all of the provinces had completed the PIC transition process. At the request of the GoI, however, a new Joint Sub-Committee for Provincial Security was formed under the auspices of the SA to assess conditions in the remaining five Iraqi provinces that did not transition to PIC before 1 January 2009. This sub-committee met for the first time in January 2009.
Iraqi insurgency
[edit]After the 2003 invasion, an insurgency developed against Coalition forces during as part of the Iraq War. The first phase of the insurgency began shortly after the invasion and lasted until the establishment of a provisional Iraqi government, and from around 2004 until May 2007 primarily targeted American-led Coalition forces. In the early months following the "end of major combat operations", insurgents conducted sniper attacks, suicide bombings at road checkpoints, and ambushes, resulting in about 112 Coalition fatalities per month.[96]
In February 2006, a sectarian civil war broke out in Iraq, leading to insurgents to direct many of their attacks against the police and armed forces of the Iraqi government. The attacks continued during the transitional reconstruction of Iraq, as the Iraqi government attempted to establish its authority throughout the country.[97][98]
Though the civil war (and the accompanying sectarian violence) ended in mid-2008, the insurgency continued after the withdrawal of US forces from Iraq in 2011, and in 2012 a renewed wave of sectarian and anti-government insurgency swept Iraq, causing thousands of casualties. Increasing violence led to another outbreak of war in Iraq in 2013, lasting until 2017.[99]
Guerrilla war
[edit]In late June 2003 there was some public debate in the US as to whether the insurgency could be characterized as a guerrilla war. On 17 June, Army Gen. John P. Abizaid said that forces in Iraq were "conducting what I would describe as a classical guerrilla-type campaign against us. It's low-intensity conflict in our doctrinal terms, but it's war however you describe it." In a statement to Congress on 18 June, Deputy Defense Secretary Paul Wolfowitz said "There's a guerrilla war there but we can win it."
Sabotage
[edit]
Sabotage of crude oil pipelines and refineries have been a key tactic of the Iraqi insurgency. The United States had intended to quickly rebuild Iraqi infrastructure for production back to pre-war levels, but widespread sabotage slowed down the pace of reconstruction. The administration has set an oil-production goal of 5,000,000 barrels per day (790,000 m3/d), but the president's numbers show that production decreased slightly in 2005 over 2004 from 2.2 million US gallons (8,300 m3) per day to 2.1 million US gallons (7,900 m3) per day. The administration claims that oil production, however, is up from 2003, when oil was produced at 1,580,000 barrels per day (251,000 m3/d).
Iraqi analysts have argued that the administration's measures are misleading because the war began in 2003, which pushed production numbers lower than they normally would have been.
"They are way off of their original projections" for where oil production would be now, said Rick Barton, an expert on Iraqi reconstruction at the Center for Strategic and International Studies in Washington. "It's basically gone nowhere in the entire time we've been there. Of course, they haven't been able to protect the pipelines. You just can't be rebuilding a country during an active war."[citation needed][100]
Fallujah
[edit]The Fallujah offensive Operation Vigilant Resolve was launched on 5 April 2004 in response to 31 March murder and mutilation of four of Blackwater's employees. Roads leading into and out of the city were closed. When the US Soldiers and Marines tried to enter, fierce fighting erupted. Members of the Iraqi insurgency opened fire with heavy machine guns, rockets, and rocket-propelled grenades. The Soldiers and Marines answered by bringing in tanks and helicopters.
The ensuing firefight resulted in a large number of casualties. Dozens of Marines were killed and injured. Two hundred and seventy-one members of the non-coalition forces were killed and 793 injured, according to official counts for the period of 5 April through 22 April. Conflicting reports leave it unclear how many of the dead and injured were rebel fighters or women and children.[101][102][103] There were also reports of ambulances and aid convoys being used by the insurgents to smuggle weapons and fighters into the city.[104] Coalition officials said that the insurgents used mosques and schools as command posts and weapon-storage facilities. A suicide-bomb-vest factory was discovered by Marines.[105]
After several failed attempts at ceasefires, the US backed out of the city. A Marine commander stated "We don't want to turn Fallujah into Dresden". The US handed authority of the city over to a former Iraqi general who had served under Saddam Hussein, and whose fighters the US acknowledges may include former members of insurgency.
Afterwards, the city was referred to as "free rebel town"; banners in the city streets proclaimed victory over the United States, and some of its mosques praised the Iraqi insurgency. The general, Muhammed Latif, told Reuters, "I want the American soldier to return to his camp. What I want more is that he returns to the United States."[106]
US marines encircled Fallujah with an earth wall, trying to control access to the city, allowing only women and children to leave the city. On 19 June 2004, twenty two Iraqis, among them women and children, were killed in a US air strike on a residential neighborhood.[107] Allawi condemned the rebellion and called upon the city to surrender Abu Musab al-Zarqawi, the leader of the Tawhid-e-Jihad group who is alleged to be hiding in Fallujah, or face aerial bombing by the United States.
Muqtada al-Sadr
[edit]On 4 April 2004, coalition forces closed Shiite cleric Muqtada al-Sadr's newspaper al-Hawza, claiming it contained incitements to violence. One example provided was that on 26 February, an article claimed that a suicide bombing in Iskandariya that killed 53 people was a rocket fired by the Americans, and not a car bomb. In response, al-Sadr launched a day of protests. During these protests, members of the Iraqi insurgency (who may or may not have been tied to al-Sadr) ambushed a Coalition patrol guarding a trash collecting unit in Sadr-City resulting in the deaths of 8 soldiers. Several dozen of al-Sadr's followers were killed during these protests.
The coalition responded by arresting one of al-Sadr's closest aides, leading to al-Sadr calling on his followers to rise up. The next days fighting erupted in many cities in southern Iraq, including Karbala, Kut, Nasiriya and Basra. The CPA announced the existence of a three-month-old arrest warrant, issued by an Iraqi judge, on al-Sadr, claiming that he was responsible for the killing of Coalition-aligned cleric Abdul Majid al-Khoei. The warrant itself inspired further opposition, as Khoei's own followers blamed Ba'athists for the murder, the Coalition-appointed Iraqi Minister of Justice stated that he had no knowledge of the warrant, and the Iraqi Jurists Association declared the warrant "illegal". Al-Sadr, who had previously created his own parallel government and a militia called the al-Mahdi Army, instructed his followers to no longer follow along with the occupation, and suggested that they attack Coalition soldiers, and his followers took control of several southern cities, often with the support of local authorities and police.
During the first few days of the uprising al-Sadr stayed in Kufa, where he traditionally had a large following. On 7 April he moved to Najaf, into a building close to the shrine of the Imam Ali, the holiest shrine in the Shia faith. After fierce fighting during the first days of the uprising, his followers took control over many cities in southern Iraq. In Kut the Ukrainian occupational contingent was forced out of the city by a rain of mortar fire. The Italians were contained inside their base in Nassiriya, and in Basra the governor's palace was occupied. In Karbala, Polish and Bulgarian forces were able to hold their own after a battle lasting the whole night. The Alliance reacted by dispensing a reactionary force on 8 April to Kut, forcing al-Sadr followers to melt away into the city's population. The same happened in most of the other cities and control was nominally ceded. Only Najaf and Kufa, which the Americans did not enter, remained effectively under the control of al-Sadr followers. The Coalition sent 2,500 US Marines to Najaf to try to 'arrest or kill' al-Sadr.
Initially hopeful that al-Sistani would force al-Sadr to capitulate, the coalition was disappointed when, while he called for all sides to show restraint, he focused instead on condemning coalition activities in Fallujah. In mid-May 2004, a US lead force began pushing into Najaf. In the process, they invaded several mosques to seize weaponry, and there were reports of damage to some of Shia Islam's holiest shrines. US forces, using their superior firepower and air support, inflicted a steady stream of al-Mahdi army casualties; al-Sadr and hospital officials disputed the numbers, and both claimed that many of them were civilians. The al-Mahdi were only able to inflict few American casualties, but on 17 May, it was reported that the Al-Madhi army drove Italian troops from their base in Nasiriyah.[108] Ten Italians were wounded, along with 20 al-Mahdi army fighters wounded and two killed, in the assault. The base was peacefully retaken the next day in a negotiated settlement with local clan leaders.
While the Alliance continually insisted that he had little support, and there were limited clashes with the smaller SCIRI, he was seldom condemned by his more senior clerics. Islamic courts expanded their influence in areas he controlled. The Imam Ali mosque ended its call for prayers with a request for divine protection for him, and his followers were clearly large in number.[109] Many believed that al-Sistani did not speak out against al-Sadr for fear of turning Shiite against Shiite. A poll found that, in mid-May 2004, 32% of Iraqis strongly supported al-Sadr, and another 36% somewhat supported him.[110]
In August 2004, al-Sadr attempted a second rebellion, and his al-Mahdi army again incited violence, especially in the Sadr city slum area of Baghdad, and in Najaf. US forces responded by pushing into the areas of Najaf controlled by al-Mahdi, sending the militia reeling. Supported by helicopter gunships, the US military managed to kill several hundred al-Mahdi fighters, and further close in on the Iman Ali mosque, where al-Sadr had made his base. Brutal fighting raged between US troops and al-Madhi militiamen in a cemetery outside the mosque. To avoid damaging the sacred mosque in a direct raid, a political solution was sought, and a deal was struck between al-Sistani and al-Sadr ended his rebellion. In September 2004, a program encouraged al-Madhi members in Sadr city to exchange their guns into authorities for a financial compensation, and the slum was almost fully pacified.
By August 2005, al-Sadr had adopted a more conciliatory tone, along with a much lower profile, saying "I call upon all the believers to save the blood of the Muslims and to return to their homes" after an outbreak of violence between some of his followers and those of Abdul Aziz al-Hakim.[111]
Hostages
[edit]
After the fall of the Ba'ath-regime, people with varying agendas have taken foreign and Iraqi hostages, including citizens of both countries that supported and opposed the invasion. This includes citizens of Australia, Brazil, Bulgaria, Canada, China, the Czech Republic, France, India, Ireland, Israel, Italy, Germany, Japan, Jordan, Nepal, Pakistan, Poland, Romania, Russia, South Korea, Thailand, Turkey, Ukraine, the United Kingdom, and the United States of America.
The hostage-taking appears to be uncoordinated, with different groups making various demands. Some hostages are released whilst others are killed, sometimes by beheading. Several kidnappings have been claimed by the Tawhid and Jihad (The Unity of God and Holy War) Islamist group, which changed its name to "Al-Qaeda in Iraq" in October 2004. The group was run by the Jordanian-born Palestinian Abu Musab al-Zarqawi. The hostages who have been beheaded by Zarqawi's group, and possibly by Zarqawi himself, include Americans Nick Berg, Eugene Armstrong and Jack Hensley, South Korean Kim Sun-il, Shosei Koda from Japan, and Kenneth Bigley from the UK. Italian Fabrizio Quattrocchi was shot in the head, possibly by another group, as was British aid worker Margaret Hassan. According to the Committee to Protect Journalists, at least 25 journalists have been kidnapped by armed groups in Iraq since April 2004, when insurgents began targeting foreigners for abduction.
While some hostagetaking seems to be politically motivated, a large number of hostages are taken by criminals as a means of obtaining cash. Iraqis presumed to have high incomes have especially been targeted.
On the evening of 4 March 2005, the car leading Giuliana Sgrena, freshly liberated, along with two agents of the Sismi, the Italian Military Intelligence service, was fired upon by US troops. Nicola Calipari, who had negotiated the liberation of the other eight Italian hostages, was killed, while Sgrena and the other agent were wounded; see Rescue of Giuliana Sgrena.
Fall-out
[edit]As a result of the uprisings US General John Abizaid in April 2004 requested an additional 10,000 troops be sent to Iraq after admitting that a number of Iraqi security personnel had abandoned their posts or joined the Iraqi insurgency.[112] On 16 April 2004, US Defense Secretary Donald Rumsfeld announced that he had approved General Abizaid's request and had extended the tour of roughly 20,000 soldiers, who were scheduled to be rotated out of Iraq, by three months. A fresh mass grave was found near Ramadi, containing the bodies of over 350 Iraqis.[113] It is unclear whether this mass grave contained dead civilians and/or militants.
Iraq Study Group Report
[edit]
At a news conference with the British Prime Minister Tony Blair in Washington on 6 December 2006, President George W. Bush commented the Iraq Study Group's bipartisan report assessing the current situation of the US-led Iraq War and making policy recommendations. President Bush admitted for the first time that a "new approach" is needed in Iraq, that the situation in Iraq is "bad there" and that the task ahead was "daunting".[114] President Bush said he would not accept every recommendation by the ISG panel but promised that he would take the report seriously.[115]
Iraq Coalition members departures
[edit]All foreign troops have withdrawn from Iraq.
American withdrawal
[edit]On 18 August 2010 the 4th Stryker Brigade, 2nd Infantry Division, the last US combat brigade withdrew from Iraq, ending the US combat mission in Iraq. 52,600 US military personnel remained in Iraq to take on an advisory role.[116]
On 19 August 2010, US President Barack Obama announced that all US combat operations would end on 31 August. 50,000 troops would stay in an advise-and-assist role. The full withdrawal was in December 2011. Between 15 and 18 December, the last troops left.
US military patrolling
[edit]During the "post-war" Iraq occupation, occupying forces have turned their attention to enforcing order through patrolling. These patrols faced insurgents who conduct ambushes using assault rifles, rocket propelled grenades, and carefully placed and timed explosives. The patrols require armored vehicles capable of stopping at least small arms fire of 7.62 mm machine gun rounds along with mandatory external weapons platforms and tracking equipment. Experience is also key in detecting any potentially threatening, out of place car, box or person while following the rules of engagement that dictate a passive-but-ready posture. Patrolling soldiers spend nearly eight hours a day in sector and accrue nearly 30 patrols per month.[citation needed]
US permanent facilities
[edit]In October 2004, Iraq's interim government transferred to US ownership 104 acres (0.42 km2) of land beside the Tigris River in Baghdad for construction of a new US embassy. The new facility will be the largest of its kind in the world, the size of Vatican City, with the population of a small town, its own defense force, self-contained power and water. A few details of the embassy complex are available from a US Senate Foreign Relations Committee report, though many of the details remain secret. Its construction is budgeted at $592 million.[117]
Besides the embassy complex, four "super bases" are being built for permanent deployment. One would be adjacent to Baghdad, two would be close to the southern and northern oil fields and the fourth would be in the west towards Syria.[118]
The US is in the process of building 14 bases known as enduring bases. Four are unknown as to name and location. The other ten are: Green Zone in Baghdad, Camp Anaconda at Balad Airbase, Camp Taji in Taji, Camp Falcon-Al-Sarq in Baghdad, Post Freedom in Mosul, Camp Victory-Al Nasr at Baghdad Airfield, Camp Marez at Mosul Airfield, Camp Renegade in Kirkuk, Camp Speicher in Tikrit and Camp Fallujuh.[119][120]
Cultural dimensions
[edit]As cultural scientist Roland Benedikter poses in his book on Sustainable Democratization of Iraq[121] and in a series of essays,[122] one main cause of the ongoing problems of pacification seems to consist in the fact that the socio-cultural dimensions of sustainability, including questions of ethnicity, religion and minority issues, have not been included appropriately in the overall democratization strategies so far.[citation needed]
See also
[edit]- Archaeological looting in Iraq: Since the fall of Saddam Hussein's regime, looters have descended upon many archaeological sites, and have begun destroying them and looting artifacts to an alarming degree.
- Criticism of the Iraq War: A list of common criticisms of the 2003 invasion and subsequent military occupation of Iraq.
- Hillbilly armor: a US military slang term coined during the occupation to refer to the improvised vehicle armor being used by some US troops.
- Human rights in post-invasion Iraq: Various parties expressed concern about the state of human rights in Iraq after the 2003 occupation of Iraq.
- Iraq and weapons of mass destruction: The Iraqi government's use, possession, and alleged intention of acquiring more types of weapons of mass destruction (WMD) during the reign of Saddam Hussein.
- United Nations Security Council and the Iraq War: Actions associated with the Gulf War in 1991 and UN Security Council Resolution 1441 in late 2002–2003 with at least 14 other resolutions and 30 statements between those two events.
- Iraq War order of battle: Current list of US and allied military formations and units involved in Iraq.
- Ibn Sina Hospital
- Iraq disarmament crisis: Issue of Iraq's disarmament reached a crisis in 2002–2003, after demands of the complete end to Iraqi production and use of weapons of mass destruction and that Iraq comply with UN Resolutions requiring UN inspectors unfettered access to areas those inspectors thought might have weapons production facilities.
- Iraq Survey Group: A fact-finding mission sent by the coalition after the 2003 Invasion of Iraq to find weapons of mass destruction (WMD) programs developed by Iraq under the regime of former Iraqi President Saddam Hussein.
- Japanese Iraq Reconstruction and Support Group: Japanese government's deployment of troops to Iraq.
- Dover test: Informal test and a journalistic phrase to describe whether the general population is supporting a military action by the public reaction to returning war casualties.
- Timeline of the Iraq War: Timeline of events during Multinational force's occupation of Iraq, following 2003 invasion of Iraq, and relevant quotations about nature of occupation from officials
- Iraq War order of battle 2009: Overview of coalition forces in Iraq.
- War on Terror (in US foreign policy circles, the global war on terrorism or GWOT) is a campaign by the United States and some of its allies to rid the world of terrorist groups and to end state sponsorship of terrorism.
- 256th Infantry Brigade Combat Team (United States)
Post World War II occupations:
- Occupied Japan: The post World War II US occupation of Japan 1945–1952
- United States Army Military Government in Korea: US military administered southern Korea from 1945 to 1948
- Morgenthau Plan: The post World War II US occupation of part of Germany 1945–1955 (Germany was not fully sovereign until 1991)
- History of Germany since 1945
- GARIOA Government And Relief in Occupied Areas of Europe
- Marshall Plan
References
[edit]- ^ "Law of Administration for the State of Iraq for the Transitional Period". 8 March 2004. Archived from the original on 9 March 2004.
- ^ a b Knut Dörmann, Laurent Colassis. "International Humanitarian Law in the Iraq Conflict" (PDF). International Committee of the Red Cross. p. 3-9.
- ^ Laws of War: Laws and Customs of War on Land Archived 25 May 2015 at the Wayback Machine (Hague IV); 18 October 1907. The Avalon Project, Yale Law School
- ^ Iraq Resolution Endorses Plan for Transition, Elections Archived 19 September 2013 at the Wayback Machine. UN Security Council Resolution 1546, 8 June
- ^ MacAskill, Ewen, Richard Norton-Taylor, and Rory McCarthy, "US and UK look for early way out of Iraq". The Guardian, 22 January 2005
- ^ Iraq Bill Demands US Troop Withdraw Archived 14 May 2013 at the Wayback Machine Associated Press, Fox News, 10 May 2007
- ^ "Iraqi parliament wants say in extension of US-led forces". The Jerusalem Post. Associated Press. 5 June 2007. Archived from the original on 29 April 2011.
- ^ Davidson, Adam (14 April 2018). "Michael Cohen and the End Stage of the Trump Presidency". The New Yorker. Archived from the original on 18 April 2018. Retrieved 19 April 2018.
- ^ Baker, David R., "Bechtel nowhere near done Archived 18 June 2009 at the Wayback Machine; Reconstruction in Iraq going slowly – airports patched up, but water, power way behind". San Francisco Chronicle, 17 April 2004.
- ^ Foreman, Jonathan, "Bad Reporting in Baghdad Archived 17 October 2015 at the Wayback Machine". News Corporation, Weekly Standard, 12 May 2003, Volume 008, Issue 34. (Originally in 12 May 2002 issue: You have no idea how well things are going.)
- ^ "Looters ransack Baghdad museum Archived 22 September 2005 at the Wayback Machine – Thousands of valuable historical items from Baghdad's main museum have been taken or destroyed by looters." BBC, 12 April 2003.
- ^ Meier, Barry, "Aftereffects: Relics; Most Iraqi Treasures Are Said to Be Kept Safe". The New York Times, Late Edition – Final, Section A, Page 20, Column 1, 6 May 2003.
- ^ Bogdanos, Matthew, (Marine Col.) (10 September 2003). "Briefing on the Investigation of Antiquity Loss from the Baghdad Museum". United States Department of Defense. Archived from the original on 10 February 2004.
{{cite web}}: CS1 maint: multiple names: authors list (link) - ^ MacFarquhar, Neil (2003), Hussein's 2 Sons Dead in Shootout, US Says, The New York Times, 23 July 2003, p. A1: "United States troops surrounded the house today and killed the two men in a ferocious shootout...."
- ^ a b Thompson, Mark. "How Disbanding the Iraqi Army Fueled ISIS". Time. Retrieved 8 October 2017.
- ^ Steele, Jonathan, "Why the US is Running Scared from Elections in Iraq Archived 16 January 2013 at the Wayback Machine". The Guardian, 19 January 2004.
- ^ Dominick, Brian, "US Forces Bombard Holy Site After Al-Sadr Offers to Leave Archived 25 October 2005 at the Wayback Machine". The NewStandard, 20 August 2004.
- ^ Miklaszewski, Jim, "cleared in mosque shootings probe; Military concludes3 unarmed insurgents were slain in self-defense". NBC News, 4 May 2005.
- ^ Carter Malkasian. "A Thin Blue Line in the Sand, article by Carter Malkasian. DemocracyJournal, issue No. 5, Summer 2007". Democracyjournal.org. Archived from the original on 27 October 2010. Retrieved 17 October 2010.
- ^ "US to pull out 15,000 from Iraq Archived 3 December 2017 at the Wayback Machine; The US is to withdraw about 15,000 troops from Iraq from next month, the deputy defence secretary has announced". BBC News, 4 February 2005.
- ^ Wright, Robin, and Ellen Knickmeyer, "US Lowers Sights On What Can Be Achieved in Iraq Archived 14 December 2017 at the Wayback Machine; Administration Is Shedding 'Unreality' That Dominated Invasion, Official Says". The Washington Post, 14 August 2005.
- ^ MacAskill, Ewen (24 September 2005). "Country is hurtling towards disintegration, Saudis warn". The Guardian. ISSN 0261-3077. Retrieved 12 March 2023.
- ^ Pleming, Sue,"US rejects Saudi view Iraq near disintegration". Archived from the original on 22 November 2005. Retrieved 24 September 2005.
{{cite web}}: CS1 maint: bot: original URL status unknown (link). Reuters, 23 September 2005. - ^ "Baghdad official who exposed executions flees". The Guardian. London. Archived from the original on 18 April 2006.
- ^ Stockman, Farah; Bender, Bryan (2 April 2006). "Iraqi militia's wave of death". The Boston Globe. Archived from the original on 20 April 2006. Retrieved 6 May 2006.
- ^ "Iraq head urges end to bloodshed". BBC News. 10 May 2006. Archived from the original on 22 December 2006. Retrieved 6 January 2010.
- ^ "A Switch in Time: A New Strategy for America in Iraq". Archived from the original on 8 October 2007.
- ^ Ottaway, Marina. "Back From the Brink: A Strategy for Iraq". Carnegie Endowment for International Peace.
- ^ "The Next Iraqi War? Sectarianism and Civil Conflict". Archived from the original on 28 February 2006.
- ^ "America's role in nation-building – from Germany to Iraq" (PDF). Archived from the original on 11 March 2006.
- ^ "Khalilzad Admits US Unlocked Pandora's Box in Iraq". Archived from the original on 11 February 2012.
- ^ "Iraq province power transferred". BBC News. 13 July 2006.
- ^ Hamid Fadhil (13 July 2006). "Iraq takes over province, clashes in Baghdad". The Boston Globe. Reuters.[dead link]
- ^ Gravelle, Dennis, "Iraqi government takes over Mosul base Archived 29 August 2006 at the Wayback Machine". MNF-Iraq.com, 21 July 2006.
- ^ Campbell, L.C., "US Troops Restore Base to Hand Back to Iraqis Archived 5 January 2014 at the Wayback Machine". defendamerica.mil, 26 May 2006.
- ^ Paley, Amit R., "British Leave Iraqi Base; Militia Supporters Jubilant Archived 16 December 2018 at the Wayback Machine". The Washington Post, 25 August 2006.
- ^ Colvin, Ross, "British troops adopt WWII tactics Archived 11 February 2007 at the Wayback Machine". Reuters, 24 August 2006.
- ^ Paley, Amit R., "Looters Ransack Base After British Depart Archived 16 December 2018 at the Wayback Machine". The Washington Post, 26 August 2006.
- ^ "Fierce battles in south Iraq city Archived 5 September 2006 at the Wayback Machine". BBC- News, 28 August 2006.
- ^ Attack on Iraqi City Shows Militia’s Power Archived 23 November 2009 at the Wayback Machine – New York Times, 20 October 2006.
- ^ a b Griffis, Margaret (9 November 2006). "Thursday: 104 Iraqis Killed, 203 Injured". Antiwar.com Original. Archived from the original on 3 March 2016. Retrieved 12 March 2023.
- ^ "Suicide bomber attacks police recruitment center". CNN. 12 November 2006. Archived from the original on 31 August 2012. Retrieved 22 September 2012.
- ^ "Suicide bomber attacks police recruitment center". CNN. 12 November 2006. Archived from the original on 31 August 2012. Retrieved 22 September 2012.
- ^ a b c "Iraq captures al Qaeda deputy". Television New Zealand. Reuters. 4 September 2006. Archived from the original on 20 September 2011. Retrieved 4 November 2011.
- ^ "Inmates transferred out of Abu Ghraib as coalition hands off control". The Boston Globe. Associated Press. 3 September 2006. Archived from the original on 17 February 2007.
- ^ "Iraq assumes command of military today". USA Today. Associated Press. 7 September 2006.
- ^ Thomas E. Ricks; page A01 (11 September 2006). "Situation Called Dire in West Iraq; Anbar Is Lost Politically, Marine Analyst Says. (Page A01)". The Washington Post. Archived from the original on 25 October 2017. Retrieved 12 September 2006.
{{cite news}}: CS1 maint: multiple names: authors list (link) CS1 maint: numeric names: authors list (link) - ^ Peter Graff (12 September 2006). "Marines deny losing Iraq's biggest province". The Washington Post. Reuters. Retrieved 12 September 2006.[dead link]
- ^ "Iraq takes over security responsibility for southern Dhi Qar province from Italian troops". Associated Press. 21 September 2006.[dead link]
- ^ Nancy Trejos; Saad Sarhan (21 December 2006). "US Transfers Control of Najaf Province to Iraqi Security Forces". The Washington Post. Archived from the original on 1 March 2017. Retrieved 29 August 2017.
- ^ Ferguson, Barbara (11 September 2007). "Petraeus Says Iraq Troop Surge Working". Arab News. Retrieved 26 December 2009.
- ^ Iraq Bill Demands US Troop Withdraw Archived 14 May 2013 at the Wayback Machine Associated Press, Fox News, 10 May 2007
- ^ BBC NEWS 21 February 2007, Blair announces Iraq troops cut Archived 5 December 2016 at the Wayback Machine
- ^ "Blair announces Iraq troop pullout". Al Jazeera. 21 February 2007. Archived from the original on 23 February 2007.
- ^ Michaels, Jim (22 May 2008). "Iraqi forces load up on US arms". USA Today. Archived from the original on 14 March 2012. Retrieved 17 October 2010.
- ^ Cole, August (5 September 2008). "Iraq Seeks F-16 Fighters". The Wall Street Journal. Archived from the original on 13 May 2013. Retrieved 17 October 2010.
- ^ "Business as usual for US arms sales". Asia Times. 24 September 2008. Archived from the original on 24 July 2009. Retrieved 17 October 2010.
{{cite web}}: CS1 maint: unfit URL (link) - ^ Scott Wilson (17 September 2009). "Biden Pushes Iraqi Leaders on Vote Law, Oil-Bid Perks". The Washington Post. Archived from the original on 8 November 2012. Retrieved 17 September 2009.
- ^ Karen Travers (16 September 2009). "In Baghdad, Biden Affirms US Commitment to Troop Withdrawal Deadlines". ABC News. Archived from the original on 25 September 2009. Retrieved 17 September 2009.
- ^ "Last full US combat brigade leaves Iraq". Archived from the original on 20 August 2010. Retrieved 18 August 2010.
- ^ "Iraq Coalition Troops; Non-US Forces in Iraq Archived 17 October 2015 at the Wayback Machine". Global Security, 16 August 2005.
- ^ "mnf-iraq.com". ww38.mnf-iraq.com. Archived from the original on 17 December 2008.
- ^ Borger, Julian, "US plans military rule and occupation of Iraq; Saddam would be replaced by General Tommy Franks". The Guardian, 12 October 2002.
- ^ Map of Iraq and Coalition forces Archived 13 January 2004 at the Wayback Machine. BBC News (GIF format).
- ^ "IRAQ: Electricity almost back to pre-war levels". Archived from the original on 30 April 2005. Retrieved 1 December 2005.
{{cite web}}: CS1 maint: bot: original URL status unknown (link). United Nations, 2 March 2004. - ^ "Iraq electricity surpasses pre-war levels Archived 22 November 2005 at the Wayback Machine". Iraq Directory, 28 July 2005.
- ^ Brown, Michelle (September 2005). ""Setting the Conditions" for Abu Ghraib: The Prison Nation Abroad". American Quarterly. 57 (3): 973–997. doi:10.1353/aq.2005.0039. JSTOR 40068323. S2CID 144661236.
- ^ Smeulers, Alette; van Niekirk, Sander (2009). "Abu Ghraib and the War on Terror - A case against Donald Rumsfeld?" (PDF). Crime, Law and Social Change. 51 (3–4): 327–349. doi:10.1007/s10611-008-9160-2. S2CID 145710956.
After the pictures were published the Bush administration was quick to condemn the abuse and accuse the low ranking soldiers who featured in the pictures. Secretary of Defense Rumsfeld described the abuse at Abu Ghraib as an isolated case and President Bush talked about: 'disgraceful conduct by a few American troops who dishonoured our country and disregarded our values.' The abuse however did not constitute isolated cases but represented further proof of a widespread pattern.
- ^ Wright, Robin, and Walter Pincus, "US, UN Seek New Leaders For Iraq Chalabi and Others Coalition Relied on May Be Left Out". The Washington Post, 24 April 2004; Page A01.
- ^ "Canada barred from Iraq contracts Archived 4 April 2004 at the Wayback Machine". Associated Press, 9 December 2003.
- ^ "Halliburton won deal after auditor warns Pentagon saw 'systemic' problems with contracts". Financial Times, 11 March 2004.
- ^ "Cheney may still have Halliburton ties Archived 26 January 2021 at the Wayback Machine Congressional report finds Vice President still has financial interest in his old company". CNN, 25 September 2003.
- ^ Jehl, Douglas, "Pentagon Finds Halliburton Overcharged on Iraq Contracts". The New York Times, 11 December 2003. Archived 17 November 2015 at the Wayback Machine
- ^ Kelley, Matt, "Bid rigging, fraud and damage common in Iraq". Associated Press, 27 April 2004.
- ^ "Evidence Of Waste Of US Taxpayers' Dollars In Iraq Contracts Archived 6 April 2004 at the Wayback Machine". Middle East Economic Survey, VOL. XLVI No 40, 6 October 2003 (ed., text of a letter sent by Representative Henry A Waxman (D-Calif) to Joshua Bolten, Director, Office of Management and Budget on 26 September.)
- ^ Hedges, Michael; Ivanavich, David (5 October 2003). "Iraqis say contract bidding is rigged: US lawmaker calls for inquiry". Houston Chronicle. Archived from the original on 6 June 2004.
- ^ "Iraq reconstruction funds missing Archived 12 January 2006 at the Wayback Machine; Almost $9bn (£4.7bn) of Iraqi oil revenue is missing from a fund set up to reconstruct the country". BBC News, 30 January 2005.
- ^ Wright, Robin, and Ellen Knickmeyer, "US Lowers Sights On What Can Be Achieved in Iraq Archived 14 December 2017 at the Wayback Machine; Administration Is Shedding 'Unreality' That Dominated Invasion, Official Says". The Washington Post, 14 August 2005; A01.
- ^ Glanz, James (25 January 2006). "Audit Describes Misuse of Funds in Iraq Projects". The New York Times. Archived from the original on 23 September 2014. Retrieved 2 July 2014.
- ^ Glanz, James (2007), "Inspectors Find Rebuilt Projects Crumbing in Iraq; Quick Deterioration Seen; Iraqis Share the Blame at Sites Where the US Declared Success." The New York Times, 29 April 2007, p. 1
- ^ "Iraq buys 250 MW/day from UAE to boost power supply". Al Arabiya News. Reuters. 15 April 2012. Archived from the original on 15 April 2012. Retrieved 14 April 2012.
- ^ Hugh Gusterson (2 February 2012). "An education in occupation". Bulletin of the Atomic Scientists. Retrieved 16 April 2012.
In just 20 years, then, the Iraqi university system went from being among the best in the Middle East to one of the worst. This extraordinary act of institutional destruction was largely accomplished by American leaders who told us that the US invasion of Iraq would bring modernity, development, and women's rights.
- ^ "Iraqi oil production at its highest in twenty years". Archived from the original on 1 July 2012.
- ^ Weisman, Steven R., "US Is Quietly Spending $2.5 Billion From Iraqi Oil Revenue to Pay for Iraqi Projects". New York Times (Foreign Desk), 21 June 2004. (Late Edition – Final, Section A, Page 8, Column 1) Archived 23 October 2015 at the Wayback Machine
- ^ Shadid, Anthony, "In Iraqi Towns, Electoral Experiment Finds Some Success". The Washington Post, 16 February 2004.
- ^ Patrick Cockburn: "US issues threat to Iraq’s $50bn foreign reserves in military deal Archived 23 April 2018 at the Wayback Machine", The Independent, 6 June 2008.
- ^ "Handover of Muthanna Province". Archived from the original on 6 February 2012.
- ^ "Defence Secretary welcomes handover of Dhi Qar Province in Iraq – UK Ministry of Defence | Defence News". Archived from the original on 6 February 2012.
- ^ "Handover of Najaf province". Archived from the original on 6 February 2012.
- ^ "Measuring Stability and Security in Iraq - June 2007 - Section 1-Stability and Security". www.globalsecurity.org.
- ^ "Iraqi Security Forces Order of Battle: June 2007 Update | FDD's Long War Journal". www.longwarjournal.org. 6 June 2007.
- ^ a b "mnf-iraq.com". ww38.mnf-iraq.com. Archived from the original on 16 April 2021. Retrieved 15 September 2020.
- ^ "US forces hand province to Iraqis". BBC News. 23 October 2008. Archived from the original on 22 February 2014. Retrieved 18 February 2014.
- ^ "US hands province to Iraqi forces". BBC News. 29 October 2008. Archived from the original on 9 November 2008. Retrieved 18 February 2014.
- ^ "US Department of Defense". US Department of Defense.
- ^ Abdullah, T.A.J., 2006, Dictatorship, Imperialism & Chaos: Iraq since 1989, London, Zed Books
- ^ "After Mosul, Islamic State digs in for guerrilla warfare". Reuters. 20 July 2017. p. Intelligence and security officials are bracing for the kind of devastating insurgency al Qaeda waged following the 2003 US-led invasion, pushing Iraq into a sectarian civil war which peaked in 2006–2007. Retrieved 1 January 2022.
- ^ "CNN.com - Sen. Reid: Iraq devolves into 'civil war' - Jul 20, 2006". www.cnn.com. Retrieved 1 January 2022.
- ^ Mostafa, Nehal (9 December 2017). "Iraq announces end of war against IS, liberation of borders with Syria: Abadi". Iraqi News. Archived from the original on 9 December 2017. Retrieved 9 December 2017.
- ^ Simmons, Greg, "Dems Doubt Iraq Progress Archived 13 January 2007 at the Wayback Machine". Fox News, 7 December 2005.
- ^ "Iraq: US Marines Fight Insurgents in Fallujah". The Las Vegas Sun, 7 April 2004.
- ^ 600 "Iraqis killed in Falluja in one week" Archived 7 June 2004 at the Wayback Machine. 12 April 2004 – 8:52 am
- ^ "Scale of Falluja violence emerges" Archived 9 May 2004 at the Wayback Machine. BBC, 12 April 2004.
- ^ Navarro, Lourdes,"Rebels smuggle supplies into Iraqi city". Archived from the original on 15 April 2004. Retrieved 26 April 2004.
{{cite web}}: CS1 maint: bot: original URL status unknown (link). Associated Press, 12 April 2004. - ^ "Marines, insurgents wage furious battle for Fallujah" Archived 15 April 2004 at the Wayback Machine. CNN.
- ^ Chandrasekaran, Rajiv, "Gamble Brings Old Uniforms Back Into Style"[dead link]. Washington Post, 7 May 2004; Page A01.
- ^ "US defends deadly air strike". CBC. 19 June 2004. Archived from the original on 12 February 2006.
- ^ "The Sun Herald (of south Mississippi) story". Archived from the original on 6 June 2004. Retrieved 6 June 2004. (from the Knight Ridder services) about the incident over the actions of the insurgents driving the Italian troops from their base in Nasiriyah called "Libeccio" ("southwest wind").
- ^ "Once considered fringe al Sadr movement now leads anti-US fight". Boston Globe, 2005. [dead link]
- ^ Ryu, Alisha, "Poll: 32% of Iraqi Respondents Strongly Support Moqtada al-Sadr Archived 28 October 2005 at the Wayback Machine". Voice of America News (via Veterans News and Information Service), 24 May 2004.
- ^ "One-day extension for Iraq constitution Archived 13 December 2005 at the Wayback Machine; Shiites, Kurds again fail to reach consensus with Sunnis". CNN, 25 August 2005.
- ^ Hess, Pamela, (Pentagon correspondent) "DOD: Security forces disappoint in Iraq". News World Communications, 2004.
- ^ "Mass Grave of Dead Iraqi Insurgents and Civilians found". Archived from the original on 5 May 2004. Retrieved 5 May 2004.
{{cite web}}: CS1 maint: bot: original URL status unknown (link). Real Cities. (ed., Originally from Knight Ridder News Coverage of Washington and the World). - ^ Reynolds, Paul (7 December 2006). "Bush ponders next Iraq move". BBC News. Archived from the original on 15 July 2016. Retrieved 6 January 2010.
- ^ "Cracks appear between Bush and Blair over need for talks with Iran and Syria". Archived from the original on 20 July 2012.
- ^ "Goodbye Iraq: Last US Combat Brigade Heads Home". Yahoo! News. 19 August 2010. Archived from the original on 21 August 2010. Retrieved 19 August 2010.
- ^ Fadel, Leila; Star-telegram, Fort Worth (20 May 2006). "US embassy is biggest secret in Baghdad". Houston Chronicle.
- ^ "From Cold War to Long War". Archived from the original on 31 August 2006.
- ^ "If the US is ultimately leaving Iraq, why is the military building 'permanent' bases?". Archived from the original on 19 April 2007.
- ^ "Iraq Facilities". www.globalsecurity.org.
- ^ Roland Benedikter, Nachhaltige Demokratisierung des Irak? (Sustainable Democratization of Iraq? Socio-cultural perspectives), Passagen Verlag Vienna 2005 634pp
- ^ Roland Benedikter. "Overcoming ethnic division in Iraq. A practical model from Europe. In: In The National Interest, The Nixon Foundation". Inthenationalinterest.com. Archived from the original on 16 June 2013. Retrieved 22 September 2012.
Further reading
[edit]- Petersen, Roger D. (2024). Death, Dominance, and State-Building: The US in Iraq and the Future of American Military Intervention. Oxford University Press.
- "Iraq Coalition Casualty Count". Archived from the original on 28 June 2005. Retrieved 29 June 2005.
- "Non-US Forces in Iraq". GlobalSecurity.org. 15 March 2005.
- Iraq Body Count (2005). "A Dossier of Civilian Casualties in Iraq 2003–2005" (PDF). Retrieved 30 December 2008.
{{cite journal}}: Cite journal requires|journal=(help) - Gillan, AudreyMaggie (19 January 2005). "Shocking images revealed at Britain's 'Abu Ghraib trial'". The Guardian. London.
- "In Pictures: Alleged prisoner abuse near Basra". The Guardian. London. 19 January 2005. Retrieved 22 May 2010.
- "Seven soldiers charged with Iraqi's murder". The Guardian. London. 3 February 2005. Retrieved 22 May 2010.
- "Iraq timeline: 1 February 2004 to 31 December 2004". The Guardian. London. January 2005. Retrieved 22 May 2010.
- Carroll, Rory (4 February 2005). "Meet the men who Britain and the US hope will take over the battle against Iraqi insurgents – if they live long enough". The Guardian. London.
- Cordesman, Anthony (2004). "US Policy in Iraq: A "Realist" Approach to its Challenges and Opportunities".
{{cite journal}}: Cite journal requires|journal=(help) - The Road Ahead: Lessons in Nation Building from Japan, Germany, and Afghanistan for Postwar Iraq by Ray Salvatore Jennings May 2003 Peceworks No. 49 United States Institute of Peace
- Lyal S. Sunga, "Dilemmas facing INGOs in coalition-occupied Iraq", in Ethics in Action: The Ethical Challenges of International Human Rights Nongovernmental Organizations, edited by Daniel A. Bell, Cambridge University Press 2007.
- Legal status
- Lyal S. Sunga, "Can International Humanitarian Law Play an Effective Role in Occupied Iraq?", 3 Indian Society of International Law Yearbook of International Humanitarian and Refugee Law (2003) 1–21.
- Management of the Iraq Reconstruction Program
- "UN Criticizes Iraq Occupation Oil Sales". New York Times, Cash Flow, 14 December 2004.
External links
[edit]- Information on the US efforts to rebuild Iraq, with focus on the PRT program
- Back from Iraq: The Veterans' Stories Project
- Searchable timeline of Iraq occupation
- The end of Saddam Hussein Warning: Graphic Execution video
- The end of Saddam Hussein (video 2 January 8/07)- Warning: Mature content.
- About.com's An American Palace in Iraq and Four Permanent US Bases Archived 3 March 2016 at the Wayback Machine
- www.iraqanalysis.org – Information source listings and analysis on post-invasion Iraq
- Iraq Body Count – Independent database listing civilians killed in the Iraq war and occupation
- "Latest analysis on Iraq". Archived from the original on 8 February 2008. Retrieved 7 November 2007.
{{cite web}}: CS1 maint: bot: original URL status unknown (link) - FSB Iraq FrogStyleBiscuit's Iraq News and Analysis
- Iraq News Archive The White House
- Senator Byrd, Robert A Call for an Exit Door from Iraq 7 April 2004, Common Dreams News Center
- Is Iraq Another 'Vietnam'? Monthly Review, volume 56, issue 2, June 2004
- US/Iraq News Mission and Justice
- Jason Vest, "Willful Ignorance", Bulletin of the Atomic Scientists, July/August 2005. Discusses US approach to counterinsurgency in Iraq.
- Sheehan-Miles, Charles Iraq in Transition: An Examination of Iraqi resistance, terrorism, insurgency and organized crime 2005
- Americans are Losing the Victory in Europe, and Grim Europe Faces Winter of Misery Life, 7 January 1946
- Oral History Interview with General William H. Draper Jr. Chief, Economics Division, Control Council for Germany, 1945–46
- Oral History Interview with General Lucius D. Clay Deputy military governor, Germany (US) 1946; commander in chief, US Forces in Europe and military governor, US Zone, Germany, 1947–49
- MarchofWar.com – Up-to-date Iraq war clock, war quotes and slogans, plus poll
- Interview with an American Contractor in Iraq
- A Policy for Germany
- Daoud al-Qaissi, Saddam's singer executed
- The World Monuments Fund's Iraq Cultural Heritage Conservation Initiative
- Did the United States Create Democracy in Germany? James L. Payne The Independent Review, Volume 11 Number 2, Fall 2006, Analysis of the axiom that democracy can be imposed
- Bibliography: Iraq Wars: Post 2003 by Edwin Moise
- Imperial Life in the Emerald City: Inside Iraq's Green Zone by Rajiv Chandrasekaran
- Fiasco: The American Military Adventure in Iraq, 2003–2005 by Thomas E. Ricks





